Achieving Democracy
by Randy Schutt
The Dilemma of Collective Choice
Plurality Vote
How should society collectively make choices in a fair and democratic way? In the decision making system used most often in the United States, citizens periodically express their sentiment by voting for a candidate or measure. Whichever alternative receives the most votes (a plurality) is chosen. It is a simple decision system — easy to understand and seemingly fair.
Unfortunately, it is often not fair at all. For example, an election in a liberal community might have three candidates, two of whom are liberal, the third a conservative. If the liberal voters in the community split their votes between the two liberal candidates, then the conservative may win — with perhaps votes totalling 35% and 25% for the two liberal candidates and 40% for the conservative. So even though 60% of the people prefer a liberal to represent them, the conservative candidate wins the election. The decision system determines a winner, but it does not do it in a way that seems fair or democratic.
Majority Vote
To overcome this problem, the decision system can be expanded slightly to require the winner to garner more than half the votes. If there are more than two alternatives and none receives a majority in the first election, then another (runoff) election is held between the top two vote-getters.
But this system can also be problematical. For example, let’s assume there are three alternatives: X, Y, and Z and that voters prefer one alternative to another in the following way:
18% X > Y > Z
17% X > Z > Y
13% Y > X> Z
21% Y > Z > X
19% Z > X > Y
12% Z > Y > X
(This notation means 18% of the voters prefer X to both Y and Z, and these 18% also prefer Y to Z.)
In the initial election, X would receive 35% of the vote, Y would receive 34%, and Z would receive 31%. In the runoff election with the top vote-getter, X, pitted against the runner-up, Y, those who initially voted for Z would now vote for either X or Y. In this runoff election, X would receive 54% and Y would receive 46% of the total vote. X would seem to be the clear winner. But in this case, 52% of the voters actually prefer Z to X (the sum of the bottom three groups). If Y had not been an option, Z would have won in the initial election.
Note that overall:
54% X > Y (54% of voters prefer X to Y)
52% Y > Z
52% Z > X
Is this an artificially constructed example in which the voters have absurdly conflicting views? Unfortunately, this case of cyclic preferences is not at all unusual — it often occurs when people rank alternatives based on several criteria. For example, in an election for office, the main issues that concern voters might be whether to cut military spending, whether to raise income taxes on wealthy people, and whether to outlaw abortion. Candidate X might support the current level of spending on the military, oppose increasing income taxes on the wealthy, and oppose abortion. Candidate Y might also support the current level of military spending and oppose increasing income taxes, but might feel that women should be able to choose to have an abortion. Candidate Z might feel that military spending should be reduced, might favor increased income taxes on the wealthy, and, though a Catholic, might still believe that abortion should not be outlawed.
Under these circumstances, it is quite possible that people might have the preferences shown above. In fact, because there are so many issues, so many ways of perceiving the issues, and so many proposed solutions to these issues, this situation actually arises quite often.
The majority vote/runoff process has another prominent problem: it encourages voters to vote strategically (manipulatively). For example, in the case shown above, those 21% of voters who prefer Y to Z to X may realize that X (their least favorite candidate) will win if they vote in the initial election according to their preference and vote for Y. But they see that if they initially vote for Z, Z will receive 52% and win. These voters therefore have an incentive to vote their second choice rather than their first in order to ensure their last choice does not win.
Rank Order Method of Voting
To solve these problems, several more complex systems of voting have been developed. In the Rank Order Method of Voting, voters rank their first few choices. Options are then assigned a certain number of points for each time they are a first choice, a smaller number of points for being a second choice, and an even smaller number of points for being a third choice. Unfortunately, this system also can lead to strange results. Consider the case of 100 voters choosing among four candidates, A, B, C, and D. Assume these voters have the following preferences:
40 A > B > C > D
35 B > C > A > D
25 C > A > D > B
For the sake of simplicity, assume no voter has any of the 21 other preference possibilities. Let’s also assume that in this election first choice candidates receive 3 points, second choice candidates receive 2 points, and third choice candidates receive 1 point.
Under these circumstances the vote count would be as follows:
A would receive (40 x 3) + (35 x 1) + (25 x 2) = 210
B would receive (40 x 2) + (35 x 3) + (25 x 0) = 195
C would receive (40 x 1) + (35 x 2) + (25 x 3) = 185
D would receive (25 x 1) = 25
Candidate A would easily outscore the others and win the election. But what if Candidate D realized he had no chance of winning and dropped out of the race? This should not matter since D is least preferred by 75 of the voters and is low on the list of the other 25. But in this case, Candidate B would then pick up an additional (25 x 1) = 25 points from the third group of voters making her the winner with 220 points.
Or consider another variation: Assume that the group of 25 voters in the last line actually preferred D to A in their preference ranking (their preference ranking was C > D > A > B instead of C > A > D > B). This change should have no effect on the election since in either case D would lose the election by a large margin. But this change would reduce the number of points A would garner by 25 (to 185), making B the winner with 195 points.
Arrow’s Impossibility Theorem
Is there some other form of voting that will sidestep these problems? Perhaps voters could choose first between two alternatives and then have the winner of that contest compete against the next alternative (Pair-Wise Voting). Or perhaps each voter could be given a certain number of points that she can allocate to the options in any way she preferred and the option garnering the largest total would win.
Kenneth Arrow [1963] studied this question carefully and proved there was no decision system that could “rationally” choose among alternatives. Specifically, he proved that no system could meet all of the following criteria — all of which he felt were quite reasonable:
(1) Universal Scope: The decision system should be able to sort through all logically possible combinations of voter’s preferences and determine a winner. Since voters often have the kind of mixed preferences outlined in the examples above, the decision system should be able to deal with them all.
(2) Unanimity: If everyone prefers one alternative, then the decision system should choose that alternative above all others.
(3) Independence of Irrelevant Alternatives: If everyone prefers A to B, then the decision system should choose A over B regardless of how people feel about other alternatives (C or D). Especially, the results should not change depending on whether D is an available alternative.
(4) Non-Dictatorship: The decision system should not be dictated by any single person’s preference.
(5) Completeness: The decision system should always be able to compare any two alternatives and determine that one is preferred to the other. For example, a decision system that cannot produce a result when some voters have opposite preferences is not very useful.
(6) Transitivity: If the decision system determines that X is preferred to Y and Y is preferred to Z, then X should be preferred to Z. This is especially important to ensure that the chosen alternative is independent of the agenda or path by which it is reached (the order in which the alternatives are considered).
Because Arrow proved that these criteria are inconsistent, many theorists have tried to find a way to relax some of them enough to find a decision system that does work. But these attempts have failed. Their postulated decision systems work only in limited situations where the population of voters expresses only certain preferences. In most real-life situations, these decision systems are unable to provide a clear decision.
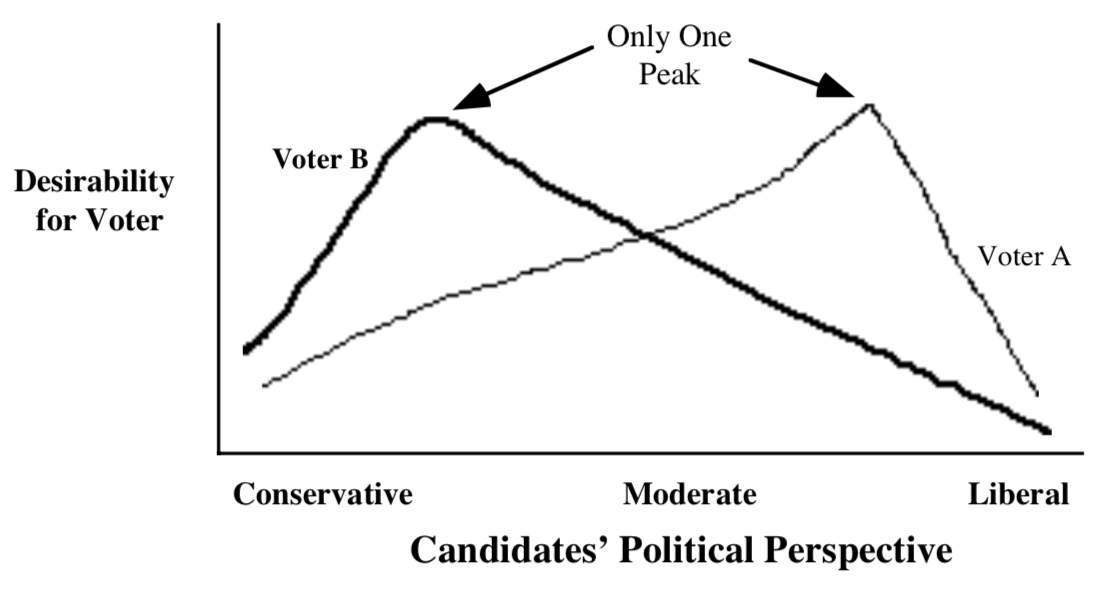
For example, majority rule works well if there are only two possible options or when everyone’s individual preferences exhibit a pattern called “single-peaked preference.” This pattern arises only when everyone evaluates the available options on a single, one-dimensional scale such as liberal-conservative or cheap-expensive. They must also prefer alternatives less and less the further they are from the alternative they value the most (see the diagram below).
Blair and Pollak [1983] reviewed the collective choice literature in which theorists have investigated relaxing each of Arrow’s criteria. They found that none of the proposed decision systems is very satisfying. The chart below shows examples of collective choice systems made possible by relaxing some of the criteria and the undesirable consequences that result.
[Picture of table]| Criterion Relaxed | Examples of Resulting Decision Rules | Undesirable Consequences |
|---|---|---|
| Unanimity | Traditional Social Code — rituals, customs, taboos | If an alternative conflicts with societal norms, it cannot be chosen even if everyone in society prefers it. |
| Non-Dictatorship | Dictatorship — one person decides for everyone Oligarchy — an elite decides for everyone |
If an alternative is not preferred by the dictator or oligarchy, it cannot be chosen even if everyone else in society prefers it. |
| Independence of Irrelevant Alternatives | Plurality Vote — highest vote-getter wins Majority Vote — highest vote-getters are matched in a run-off Rank-Order Vote — voters rank alternatives |
A minority alternative can win if the majority position is split between two or more alternatives.
Minority alternatives can pull votes from one alternative, causing it to lose when it would otherwise win. |
| Transitivity | Pair-Wise Voting — alternatives are voted on two at a time and the winners are then matched in another contest | The final outcome can differ depending on the way the alternatives are matched. |
| Transitivity (of indifference only) | Unanimity — when everyone prefers one alternative, choose that alternative
Passive Unanimity — when everyone either prefers one alternative or is indifferent, choose that alternative |
Whenever two people have opposite preferences, there can be no decision. |
Blair and Pollak conclude that the three objectives of any collective choice system — collective rationality, decisiveness, and equality of power — stand in irreconcilable conflict. “If society forgoes collective rationality, thereby accepting the necessary arbitrariness and manipulability of irrational procedures, majority rule is likely to be the choice because it attains the remaining goals. If society insists on retaining a degree of collective rationality, it can achieve equality by adopting the rule of [unanimity], but only at the price of extreme indecisiveness. Society can increase decisiveness by concentrating veto power in progressively fewer hands; the most decisive rule, dictatorship, is also the least egalitarian.”
And unfortunately, this bleak conclusion focuses only on Arrow’s six criteria. Other theorists have proposed several additional criteria that are generally valued for collective decisions in a democracy. These additional criteria make it even more difficult to come up with a fair and democratic decision system. These additional criteria include:
Anonymity: The decision should not be dependent on who has the preferences, only on the total number of people who do. “Common” people should have the same influence as “important” people.
Responsiveness to Intensity or Value of Preference: The preferences of a few people who strongly favor one option should stand with equal or even greater weight than the desires of many more people who only mildly support another option. Opinions based on expertise should be valued more than those based on whim.
Neutrality: The decision should be the same no matter who or what is affected (all other things being equal), that is, it should not be subject to irrational prejudice.
Liberality/Respect for Privacy: Personal decisions should be decided by individuals, not by anyone else. A majority should not be able to decide which clothes you can wear or who you can talk with.
Protection of Those Most Vulnerable: Decisions should be more responsive to those who would be negatively affected and those who are most vulnerable to those effects (such as poor people or oppressed minorities).
It is easy to see that these criteria pose even more irreconcilable conflicts with the previous criteria and with each other (for mathematical proofs, see Amartya Sen [1970]).
Is True Democracy Possible?
Clearly, the prospects are very poor for creating a collective choice system that can meet even a subset of these criteria. Yet the criteria all have great merit and are not easily abandoned — they are the essence of what we consider democracy. What are we to do?
Since there is no single best solution, we are free to choose a solution that best addresses a particular situation. For example, in those situations when there are only two options, a decision must be made, equality among people is important, everyone’s preferences should be valued equally, and the decision will not adversely affect anyone, then a simple majority vote is probably the best choice. Dictatorial decision-making is probably a reasonable process when decisiveness is critical and the person making the decision will also be affected by it. For example, it is reasonable for the captain of a ship caught in a storm to make dictatorial decisions.
Under other circumstances, our society has already made reasonable choices:
• Juries must unanimously vote for conviction in capital cases. Since the consequences are so dire in these circumstances, the law requires overwhelming support for a guilty verdict. But since there are only 8 or 12 people on the jury (not the whole society) it is still possible to achieve unanimity whenever the evidence is strong.
• In minor legal cases, a judge decides unilaterally.
• In the U.S. Senate, ordinary bills pass with a simple majority vote, but debate can only be cut off with a three-fifths vote, and a proposed constitutional amendment requires a two-thirds vote.
• Private decisions about what we eat or what we say are generally left for us to make individually.
Changing Preferences
There is also another acceptable way to relax the Universal Scope criterion that has not received much attention. The Universal Scope criterion demands that the collective choice system must take individual preferences and aggregate them into a single choice. As usually stated, this criterion requires that all possible sets of preferences be aggregated.
But what if we permit people to discuss and debate the issues and thereby elicit why they support their favored alternative? What if we further permit them to challenge the merits of alternatives, permit them to learn additional information about the ramifications of each, and permit them to modify and combine worthwhile alternatives? What if we permit them to change their minds?
Most groups have some process that encourages (or at least allows) these preference-changing interactions. As a result, under certain circumstances, individuals’ preferences will sometimes change and shift into alignment with others’ preferences. Moreover, some individuals’ preferences may fade to indifference — they no longer care what the final decision is. In these cases, unanimity of opinion may develop or, alternatively, everyone may be willing to consent to one option even if they do not prefer it.
In cooperative groups, decisions like this can be made even more often because individuals will look for solutions that best accommodate the group. They will focus less on their own personal desires and preferences and more on what is best for the group. Only when an option threatens to harm them or to trample their privacy do they feel compelled to block the decision process. This kind of cooperative process is usually known as “consensus decision-making.”
The consensus process is often dismissed as utopian or of limited applicability, but it actually has been used in a wide variety of situations. It is regularly practiced by Quakers (the Religious Society of Friends), many progressive social change activists, and an increasing number of others. It is also the process typically used informally by friends.
The Consensus Process
The consensus process does not focus on summing the individual preferences of people, but on coming up with good collective solutions. It pushes people to balance their own desires with the wants and needs of others. This process does not usually work well in hostile or manipulative groups or in competitive groups that are trying to allocate resources. But even in these groups, it can work since every effort to manipulate or dictate a decision just results in stagnation. Given enough time, eventually everyone realizes they must cooperate and produce a solution that is fair enough to be accepted by everyone.
The consensus process also does not usually work well in groups where individuals hold conflicting basic values. Basic values are those deep beliefs that a person applies under all circumstances. Everyone has some basic values like “I should not be killed.” As in this example, many of these values are shared by everyone. We can all understand them, and we are therefore willing to make decisions that do not violate them. Some other basic values are based on prejudice (racism, sexism, classism, and so on) or irrational fears. These are often immutable to logical or emotional appeals and can therefore lead to insurmountable disagreements.
All non-basic values, by definition, can change. New information, persuasive arguments, or emotional appeals can sway people to change their perspectives.
The consensus process works best in cooperative groups in which people value the other members of the group and wish to see them accommodated. It works best when individuals are able to rationally discuss their various perspectives and they are willing to reconsider their prejudices. And it works best when there is enough time for thorough discussion.
References
Arrow, Kenneth J., Social Choice and Individual Values, Second Edition, Yale University Press, 1963.
The first edition was published in 1951. This work carefully defines the problem of determining collective choice based on the preferences of individual members of a group. It proves that several apparently reasonable conditions of rationality and fairness are logically inconsistent: the Impossibility Theorem.
Blair, Douglas H. and Robert A. Pollak, “Rational Collective Choice,” Scientific American, Aug. 1983, p. 88.
A good summary of the voting paradox and the impossibility theorem of collective choice. It includes some of the proposed ways to relax Arrow’s conditions and how those lead to untenable solutions.
Sen, Amartya K., Collective Choice and Social Welfare, Holden Day, 1970.
A somewhat readable expansion of Arrow’s essay that explores several other proposed conditions and their limitations.
 The Vernal Project
The Vernal Project